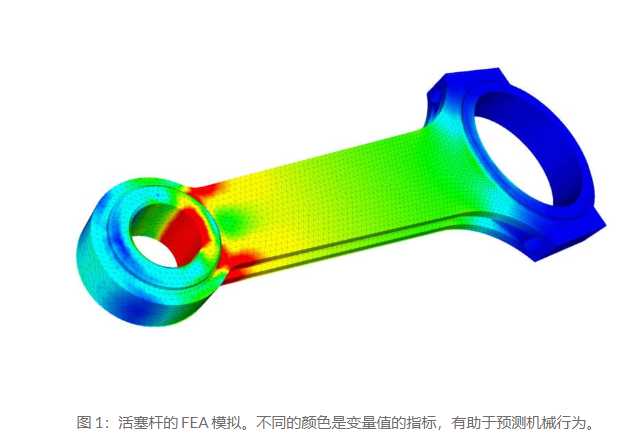
有限元分析 (FEA) 是使用称为有限元法 (FEM) 的数值技术模拟任何给定的物理现象。
工程师使用FEA减少物理原型和实验的数量,并在设计阶段优化组件,以更快地开发更好的产品,同时节省开支。
有必要使用数学来全面理解和量化任何物理现象,例如结构或流体行为、热传输、波传播、等。大多数这些过程都使用偏微分方程 (PDE) 来描述。然而,对于求解这些偏微分方程的计算机,数值技术在过去几十年得到了发展,而当今最突出的技术之一就是有限元分析。
微分方程不仅描述自然现象,也描述工程力学中遇到的物理现象。
这些偏微分方程 (PDE) 是复杂的方程,需要求解这些方程才能计算结构的相关量 以估计给定载荷下的结构行为。重要的是要知道 FEA 仅给出问题的近似解,并且是获得这些偏微分方程的真实结果的数值方法。
简而言之,FEA 是一种数值方法,用于预测零件或装配体在给定条件下的行为方式。
它被用作现代仿真软件的基础,帮助工程师找到设计中的弱点、紧张区域等。基于 FEA 方法的模拟结果通常通过色标来描述,例如显示物体上的压力分布。
分步解决
为了能够进行模拟,需要创建一个由多达数百万个共同构成结构形状的小元素组成的网格。对每个元素进行计算。结合各个结果给我们结构的最终结果。我们刚才提到的近似值通常是多项式的,实际上是对元素的插值。这意味着我们知道元素内某些点的值,但不是每个点的值。这些“特定点”称为节点,通常位于元素的边界处。变量变化的准确性由一些近似值表示,例如。线性、二次、三次等。为了更好地理解近似技术,我们将查看一维条形。
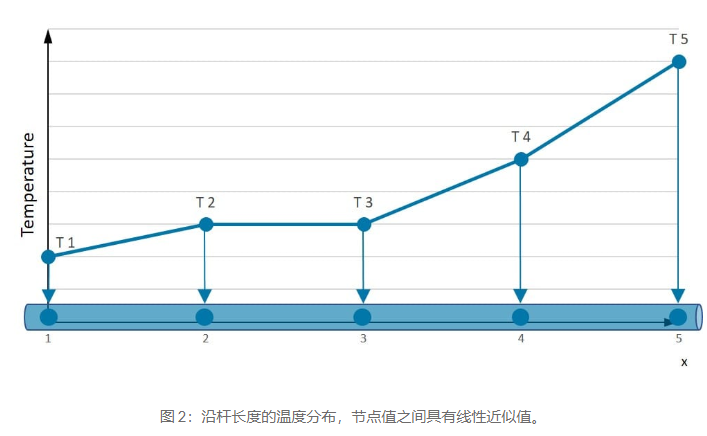
假设我们知道该条在 5 个特定位置(图中的数字 1-5)的温度。现在的问题是:我们如何预测这些点之间的温度?线性近似非常好,但有更好的可能性来表示真实的温度分布。如果我们选择平方近似,则沿条的温度分布会平滑得多。然而,我们看到,无论多项式次数如何,一旦我们知道节点处的值,杆上的分布就是已知的。如果我们有一个无限长的条,我们就会有无限多的未知数(自由度 (DOF))。但在这种情况下,我们遇到了“有限”数量的未知数的问题:
具有有限个未知数的系统称为离散系统。具有无限个未知数的系统称为连续系统。
我们在使用有限元分析时拥有的最大优势之一是我们可以改变每个元素的离散化或离散化相应的基函数。事实上,我们可以在高梯度的区域使用较小的元素你预计。为了对函数的陡度建模,我们需要进行近似。
偏微分方程
在继续进行 FEA 本身之前,了解不同类型的 PDE 及其对 FEA 的适用性非常重要。理解这一点对每个人都很重要,无论一个人使用有限元分析的动机如何。人们应该经常提醒自己,FEA是一种工具,任何工具的好坏取决于它的用户。
PDE 可分为椭圆(非常平滑)、双曲线(支持具有不连续性的解)和抛物线(描述时间相关的扩散问题)。在求解这些微分方程时,需要提供边界和/或初始条件。根据 PDE 的类型,可以评估必要的输入。每个类别中 PDE 的示例包括泊松方程(椭圆)、波动方程(双曲线)和傅里叶定律(抛物线)。
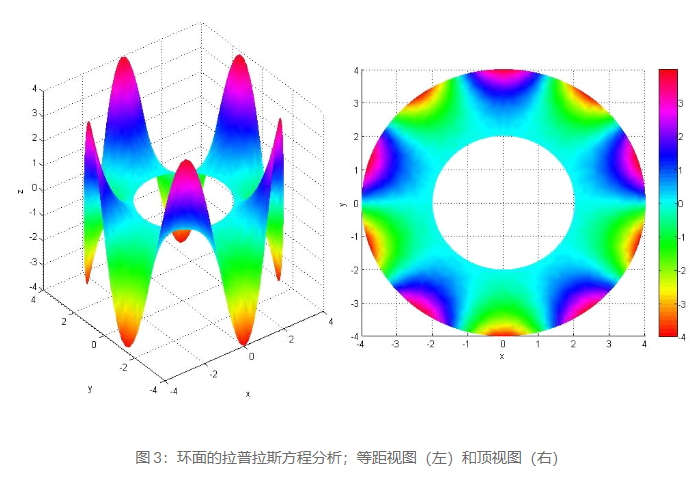
解决椭圆偏微分方程的主要方法有两种——有限差分分析 (FDA) 和变分(或能量)方法。FEA 属于变分法的第二类。变分方法主要基于能量最小化的哲学。
双曲 PDE 通常与解决方案中的跳跃相关联。例如,波动方程是双曲 PDE。由于解中存在不连续性(或跳跃),最初的 FEA 技术(或 Bubnov-Galerkin 方法)被认为不适合求解双曲 PDE。然而,多年来,已经进行了修改以扩展FEA软件和技术的适用性。
重要的是要考虑使用不适合所选 PDE 类型的数值框架的后果。这种用法会导致被称为“不正确设定”的解决方案。这可能意味着域参数的微小变化会导致解中的大振荡,或者解仅存在于域或时间的特定部分。这些都不靠谱。适定的解决方案是用唯一的解决方案定义的,该解决方案对于定义的数据连续存在。因此,考虑到可靠性,获得它们极为重要。
弱和强公式
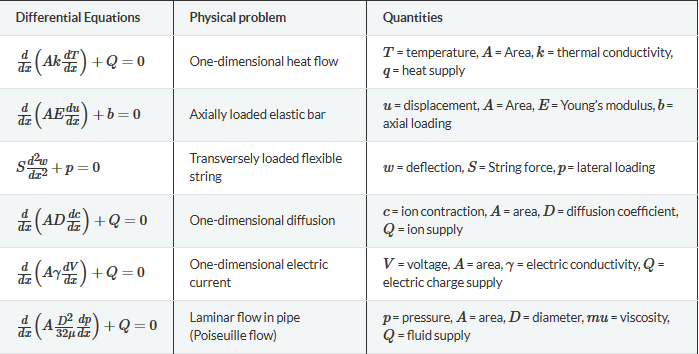
表 1:二阶微分方程
二阶偏微分方程的解要求高度平滑( x ). 这意味着位移的二阶导数必须存在并且必须是连续的!这也意味着对几何形状(尖锐边缘)和材料参数(材料中的不同模量)等参数不能受到影响的要求。
要开发有限元公式,必须以称为弱形式的积分形式重述偏微分方程。弱形态和强形态是等价的!在应力分析中,弱式称为虚功原理。
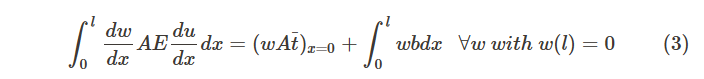
给定的方程是所谓的弱形式(在这种情况下是弹性静力学的弱公式)。顾名思义,弱形式的解不需要像强形式的解那样平滑,这意味着连续性要求较弱。
必须记住,满足弱形式的解也是方程的强对应形式的解。另外,请记住试用解决方案( x )必须满足位移边界条件。这是试验解的一个基本属性,这就是为什么我们称这些边界条件为基本边界条件。
最小势能
有限元分析也可以用变分原理来执行。在一维弹性静力学的情况下,最小势能对于保守系统是有弹性的。平衡位置是稳定的,如果系统的势能π是最小的。稳定位置的每一个无穷小干扰都会导致能量不利状态,并意味着恢复反应。一个简单的例子是立在地上的普通玻璃瓶,它的势能最小。如果它倒下,除了一声巨响,什么也不会发生。如果它站在桌子的角落并掉到地上,它很可能会摔坏,因为它会将更多的能量带向地面。对于变分原理,我们利用了这个事实。能量水平越低,得到错误解的可能性就越小。总势能π系统的功由内力(应变能)组成
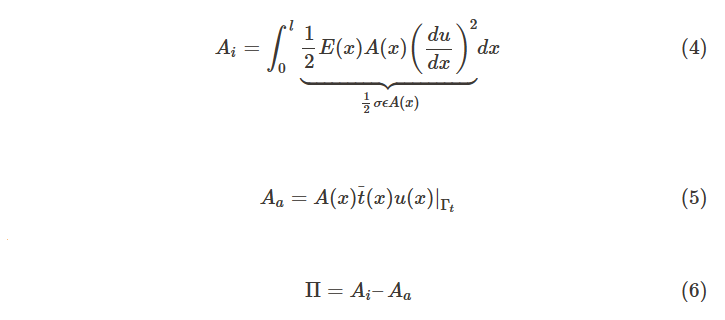
网状融合
计算力学中影响精度的最容易被忽视的问题之一是网格收敛。这与单元需要多小有关,以确保分析结果不受更改网格大小的影响。
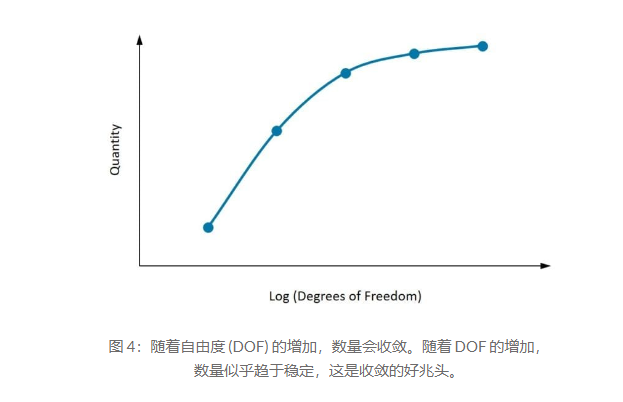
上图显示了一个数量随着自由度的增加而收敛。如图所示,首先确定感兴趣的数量很重要。至少需要考虑三个点,并且随着网格密度的增加,感兴趣的数量开始收敛到特定值。如果两个后续的网格细化没有显着改变结果,那么可以假设结果已经收敛。
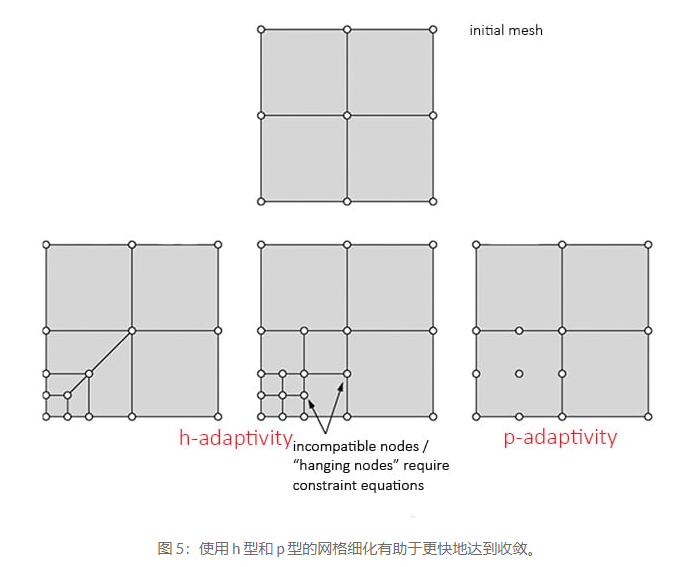
进入网格细化问题,并不总是需要细化整个模型中的网格。圣维南原理强调一个区域的局部应力不会影响其他地方的应力。因此,从物理的角度来看,模型只能在特定的感兴趣区域进行细化,并且还具有从粗网格到细网格的过渡区域。如上图所示,有两种类型的细化(h-和p-细化)。h-refinement 涉及减少元素大小,而 p-refinement 涉及增加元素的阶数。
这里区分几何效应和网格收敛很重要,特别是当使用直线(或线性)元素对曲面进行网格化时,需要更多元素(或网格细化)才能准确捕获边界。网格细化导致错误显着减少:

像这样的细化可以增加解决方案的收敛性,而不会增加要解决的整体问题的规模。
如何衡量收敛性
那么既然已经讨论了收敛的重要性,那么如何衡量收敛呢?什么是收敛的量化指标?第一种方法是与解析解或实验结果进行比较。
位移误差:
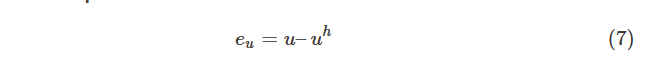
u是位移场的解析解
应变误差:
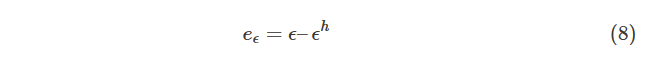
ε 是应变场的解析解
应力误差:
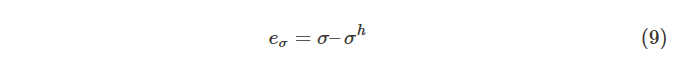
σ 是应力场的解析解
如上面的方程式所示,可以为位移、应变和应力定义多个误差。这些误差可用于比较,它们需要通过网格细化来减少。
有限元分析软件

有限元分析开始于对与航空航天和土木工程相关的几种机械应用进行建模方面的重大承诺。有限元方法的应用才刚刚开始发挥其潜力。最令人兴奋的前景之一是它在流体-结构相互作用等耦合问题中的应用;热机械、热化学、热化学机械问题压电、铁电、电磁学和其他相关领域:
静态分析
通过静态分析,您可以分析线性静态和非线性准静态结构。在施加静载荷的线性情况下,只需一步即可确定结构响应。可以考虑几何、接触和材料非线性。
动态分析
动态分析可帮助您分析在特定时间范围内经历动态载荷的结构的动态响应。要以真实的方式对结构问题进行建模,您还可以分析载荷和位移的影响。
模态分析
振动引起的结构的特征频率和特征模态可以使用模态分析进行模拟。结构或系统在给定负载下的峰值响应可以通过谐波分析来模拟。
想了解更多一些有限元仿真软件可查看: CAE概念厂商及软件介绍
不同类型的有限元方法
正如前面关于 PDE 的部分所讨论的,传统的 FEM 技术在与流体力学、波传播等相关的建模问题中表现出不足。在过去的二十年中,已经进行了多项改进以改进求解过程并扩展有限元的适用性分析广泛的问题类型。一些仍在使用的重要的包括:
扩展有限元法 (XFEM)
Bubnov-Galerkin 方法需要元素间位移的连续性。然而,接触、断裂和损坏等问题涉及有限元方法无法直接处理的不连续性和跳跃。为了克服这个缺点,XFEM 在 1990 年代诞生了。XFEM 通过使用 Heaviside 阶梯函数扩展形函数来工作。额外的自由度被分配给不连续点周围的节点,以便可以考虑跳跃。
广义有限元法 (GFEM)
GFEM 在 90 年代与 XFEM 大约同时推出。它结合了传统FEM软件和无网格方法的特点。形状函数主要在全局坐标中定义,并进一步乘以统一分区以创建局部基本形状函数。GFEM 的优势之一是防止围绕奇点重新划分网格。
混合有限元法
在一些问题中,例如接触或不可压缩性,约束是使用拉格朗日乘数施加的。这些由拉格朗日乘数引起的额外自由度是独立求解的。方程式像耦合系统一样求解。
hp-有限元法
hp-FEM 是使用自动网格细化 (h-refinement) 和增加多项式阶数 (p-refinement) 的组合。这与分别进行 h- 和 p- 优化不同。当使用自动 hp-refinement 时,一个元素被分成更小的元素(h-refinement),每个元素也可以有不同的多项式阶数。
间断伽辽金有限元法 (DG-FEM)
DG-FEM 已经显示出使用有限元的思想来解决传统有限元方法薄弱的双曲方程的重要前景。此外,它还在大多数材料工艺中常见的弯曲和不可压缩问题方面显示出希望。这里向弱形式添加了额外的约束,包括惩罚参数(以防止相互渗透)和元素之间的其他应力平衡项。
速石科技有限元分析
速石的FEA软件组件使您能够虚拟测试和预测结构的行为,从而解决受静态和动态载荷条件影响的复杂结构工程问题。FEA仿真平台使用可扩展的数值方法,可以计算数学表达式,否则由于复杂的载荷、几何形状或材料特性,这些表达式将非常具有挑战性。
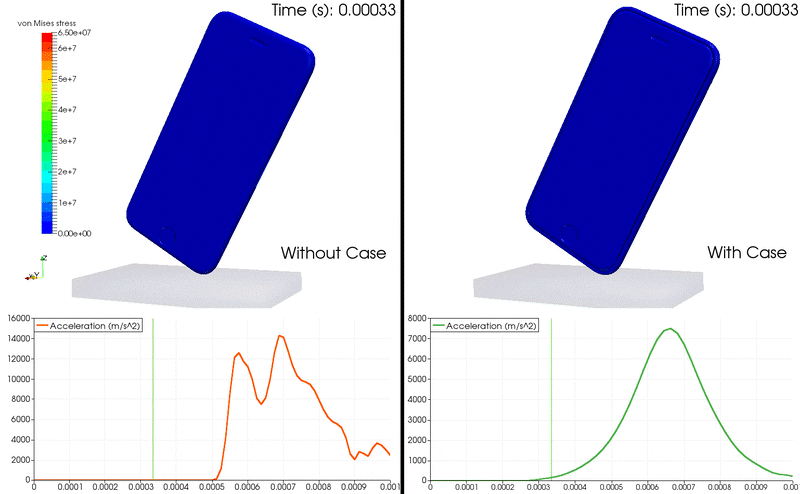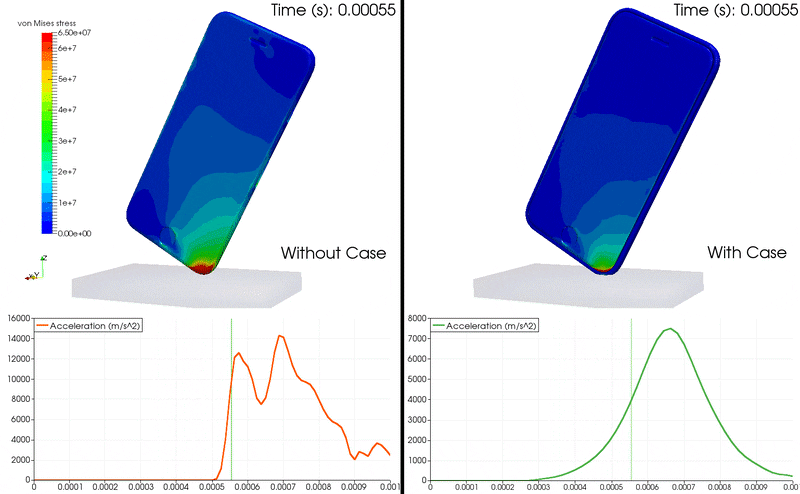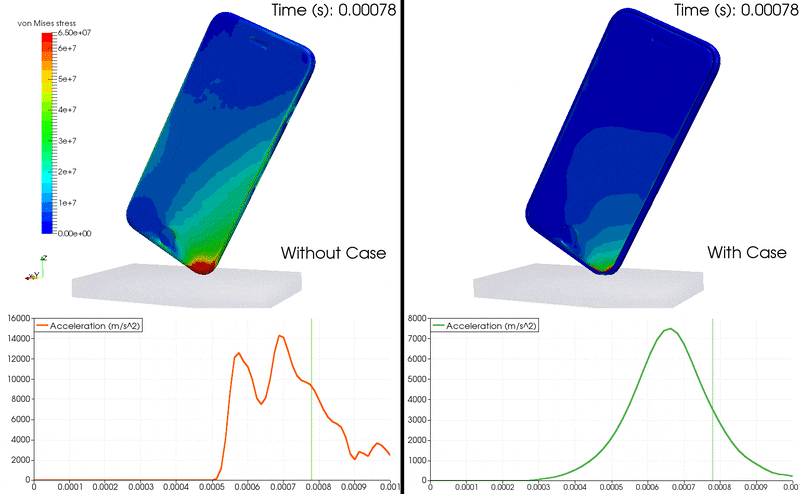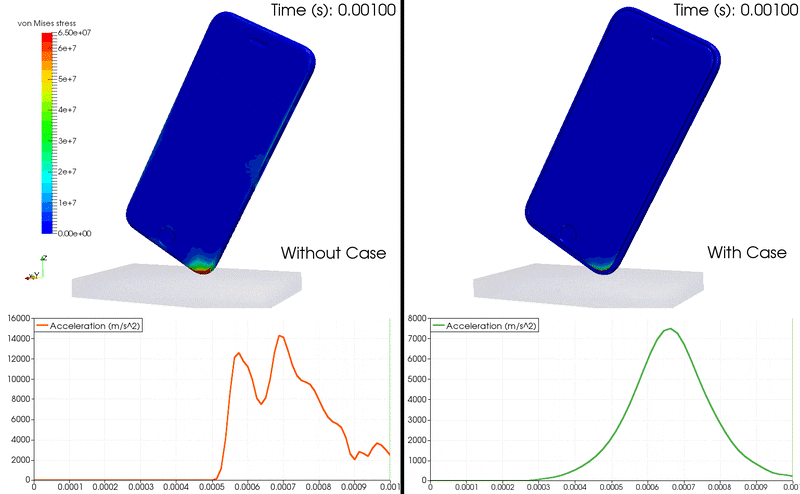
动画 1:iPhone 掉落 FEA 使用加速度图显示 von Mises 应力及其在手机内部的增长。
以上就是本篇的关于有限元的介绍,想了解更多CAE相关信息 欢迎扫码关注小F(ID:iamfastone)获取
- END -
我们有个CAE设计研发云平台
集成多种CAE应用,大量任务多节点并行
应对短时间爆发性需求,连网即用
跑任务快,原来几个月甚至几年,现在只需几小时
5分钟快速上手,拖拉点选可视化界面,无需代码
支持高级用户直接在云端创建集群
扫码免费试用,送200元体验金,入股不亏~

更多电子书 欢迎扫码关注小F(ID:imfastone)获取

你也许想了解具体的落地场景:
王者带飞LeDock!开箱即用&一键定位分子库+全流程自动化,3.5小时完成20万分子对接
这样跑COMSOL,是不是就可以发Nature了
Auto-Scale这支仙女棒如何大幅提升Virtuoso仿真效率?
1分钟告诉你用MOE模拟200000个分子要花多少钱
LS-DYNA求解效率深度测评 │ 六种规模,本地VS云端5种不同硬件配置
揭秘20000个VCS任务背后的“搬桌子”系列故事
155个GPU!多云场景下的Amber自由能计算
怎么把需要45天的突发性Fluent仿真计算缩短到4天之内?
5000核大规模OPC上云,效率提升53倍
提速2920倍!用AutoDock Vina对接2800万个分子
从4天到1.75小时,如何让Bladed仿真效率提升55倍?
从30天到17小时,如何让HSPICE仿真效率提升42倍?
关于为应用定义的云平台:
芯片设计五部曲之二 | 图灵艺术家——数字IC
芯片设计五部曲之一 | 声光魔法师——模拟IC
【ICCAD2022】首次公开亮相!国产调度器Fsched,半导体生态1.0,上百家行业用户最佳实践
解密一颗芯片设计的全生命周期算力需求
居家办公=停工?nonono,移动式EDA芯片设计,带你效率起飞
缺人!缺钱!赶时间!初创IC设计公司如何“绝地求生”?
续集来了:上回那个“吃鸡”成功的IC人后来发生了什么?
一次搞懂速石科技三大产品:FCC、FCC-E、FCP
速石科技成三星Foundry国内首家SAFE™云合作伙伴
EDA云平台49问
亿万打工人的梦:16万个CPU随你用
帮助CXO解惑上云成本的迷思,看这篇就够了
花费4小时5500美元,速石科技跻身全球超算TOP500